Domain of f(x, y) = log₂(x + y) / √x

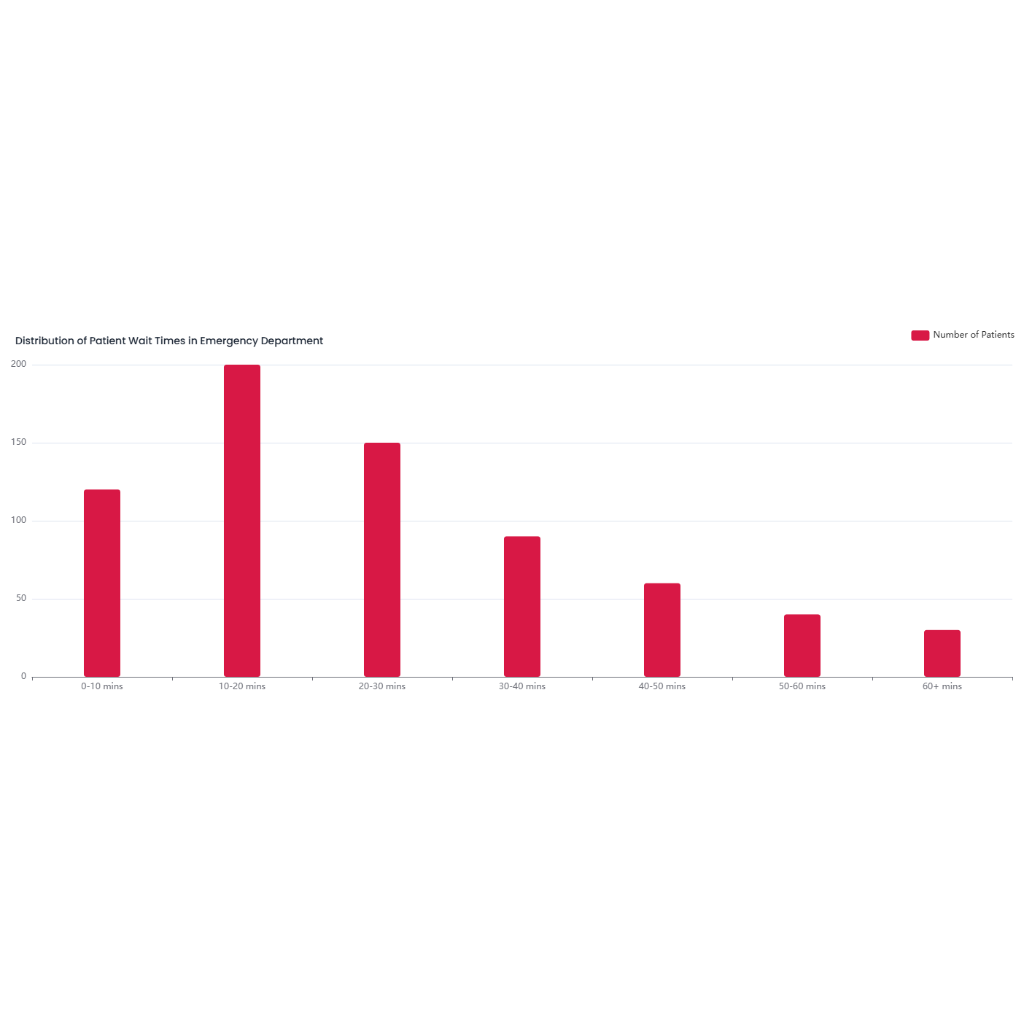
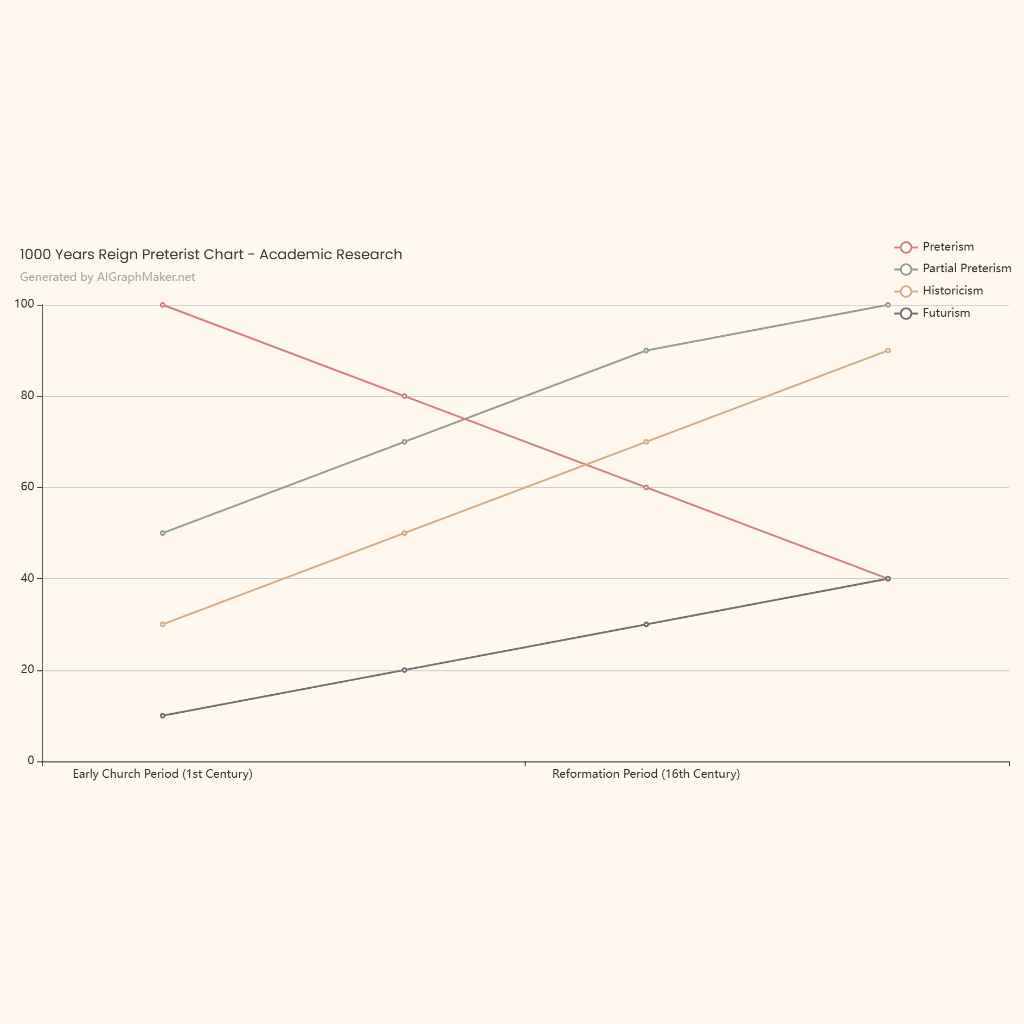
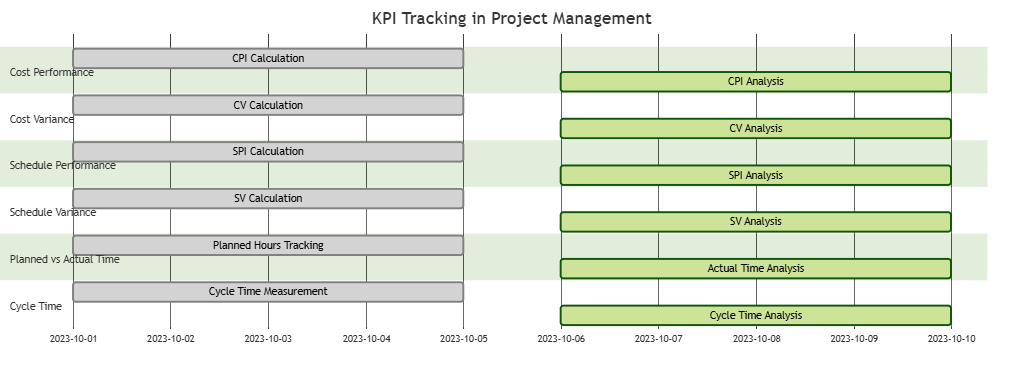
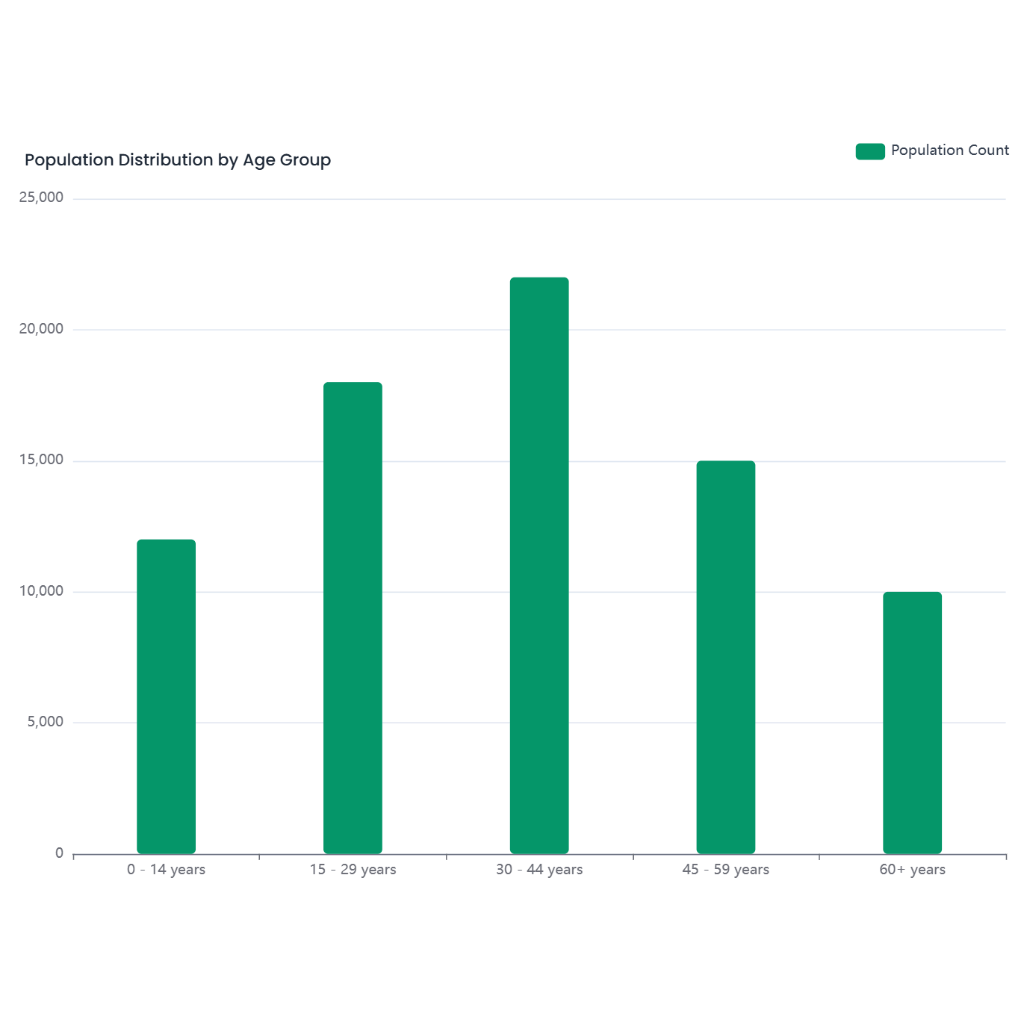
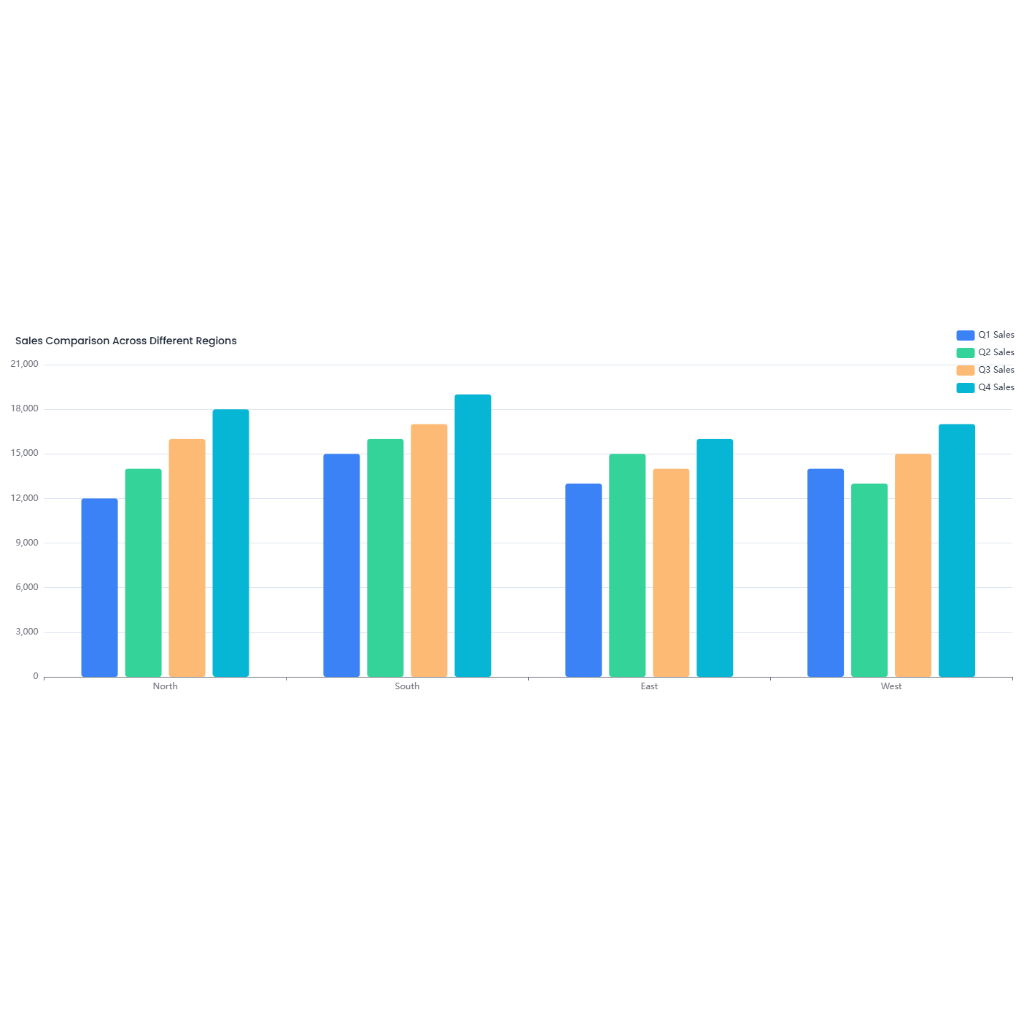
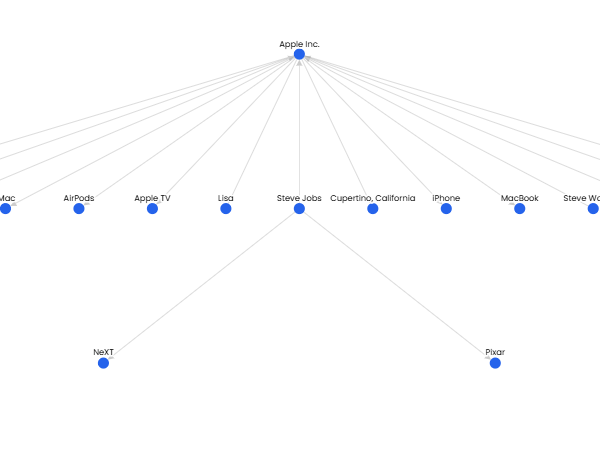
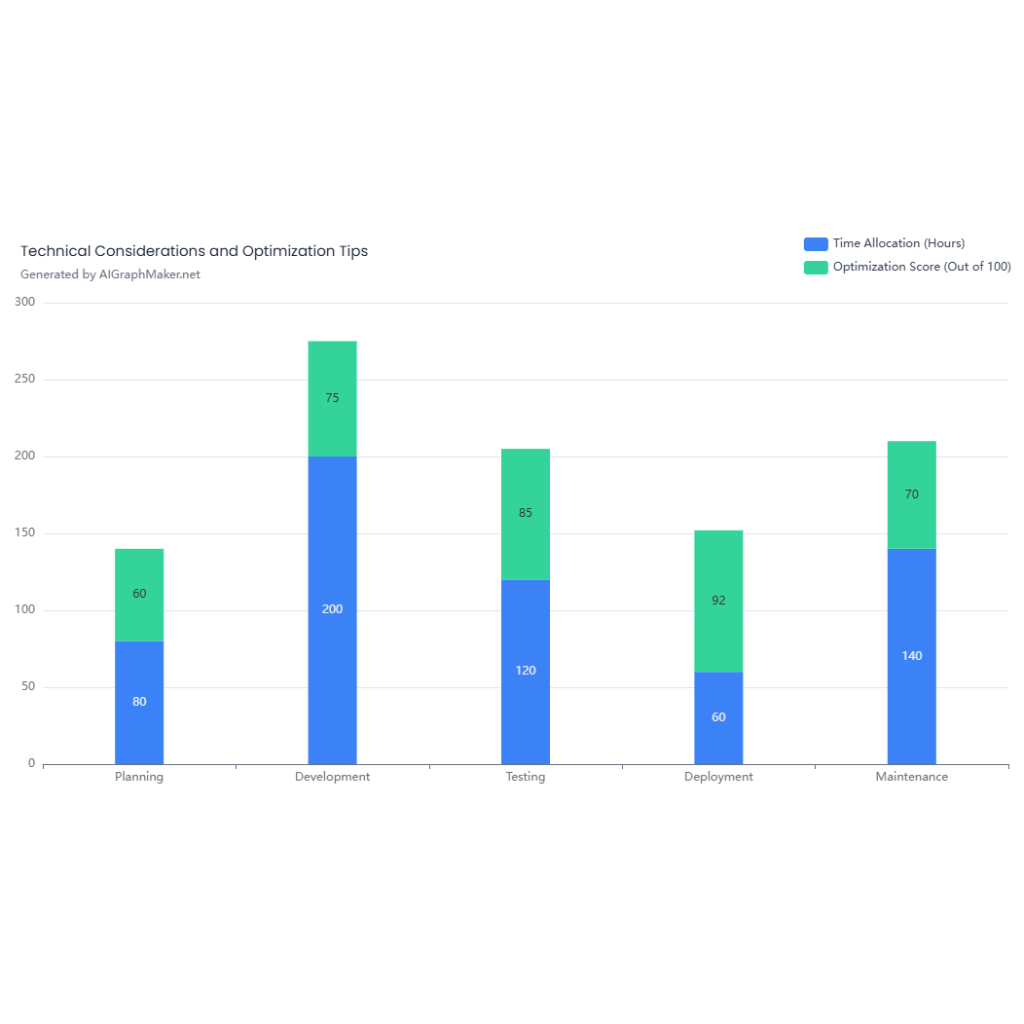
Sketching the domain of f(x, y) = \frac{\log_2 (x + y)}{\sqrt{x}}
The function is defined where:
x + y > 0 (i.e., the region above the line y = -x).
x > 0 (i.e., only the right half-plane is valid).
Final domain: The shaded region where both conditions hold, this is the region in the first quadrant and the right half of the second quadrant above the line y = -x.